CAPÍTULO 2 Medidas de desigualdade
O assunto sobre medidas de desigualdade está baseada na sua totalidade no capítulo 17 de Hoffmann (2006)
2.1 Príncipio de Pigou-Dalton
A condição de Pigou-Dalton define que as medidas de desigualdades devem ter seus valores aumentados quando há transferência regressivas de renda. Para entender a condicção de Pigou-Dalton, considere uma população com apenas duas pessoas cujas rendas são \(X_1\) e \(X_2\). Então, \(\mu = \frac{X_1 + X_2}{2}\). No caso de perfeita igualdade, \(X_1 = X_2 = \mu\). No caso de uma distribuição com \(X_1 \neq X_2\), uma transferência de renda do mais pobre para o mais rico, mantendo a renda média constante, aumenta o grau de desigualdade.
2.2 Transferência Regressiva
Essa tranferência de renda do mais pobre para o mais rico, mantida a renda média constante, é denominada como transferência regressiva de renda. Portanto, uma transferência progressiva é a transferência de renda do mais rico para o mais pobre.
2.3 Curva de Lorenz
| estrato | % no estrato da população (%) | % no estrato da renda (%) | % acumulada da população (100\(p\)) | % acumulada da renda (100\(\Phi\)) |
|---|---|---|---|---|
| I | 30 | 7 | 30 | 7 |
| II | 20 | 9 | 50 | 16 |
| III | 20 | 13 | 70 | 29 |
| IV | 10 | 10 | 80 | 39 |
| V | 10 | 16 | 90 | 55 |
| VI | 5 | 13 | 95 | 68 |
| VII | 4 | 19 | 99 | 87 |
| VIII | 1 | 13 | 100 | 100 |
Considere os dados da tabela 2.1. Na coluna de porcentagem acumulada podemos observar que 70% da população possui 29% da renda. Os percentuais acumlados da população \(p\) e da renda \(\Phi\) formam um plano cartesinao \((p,\Phi)\) originando a Cuirva de Lorenz.
library(ineq)
# usando os valores do exemplo em porcentagem
# mesmo
p <- c(30, 20, 20, 10, 10, 5, 4, 1)
r <- c(7, 9, 13, 10, 16, 13, 19, 13)
# calcula o mínimo da curva de Lorenz
Lcmin <- Lc(r, n = p)
# Desenha a curva de Lorenz em um gráfico
plot(Lcmin)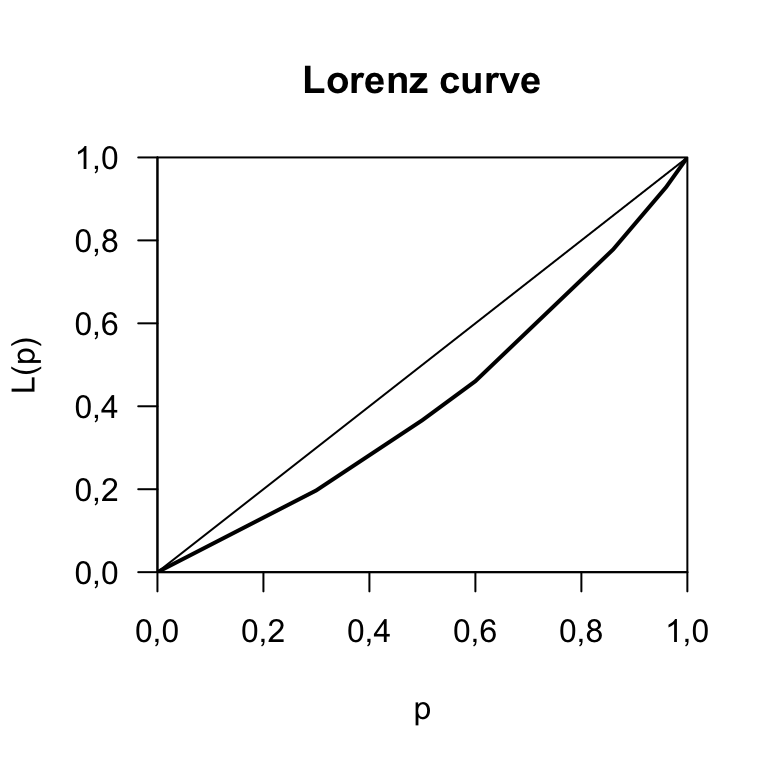
FIGURA 2.1: Curva de Lorenz
Considerando a curva de Lorenz, figura 2.2, que é basicamente a obtida pelo R, figura 2.1, mas com algumas indicações, é possível obter algumas definições.
knitr::include_graphics("lorenz3.png")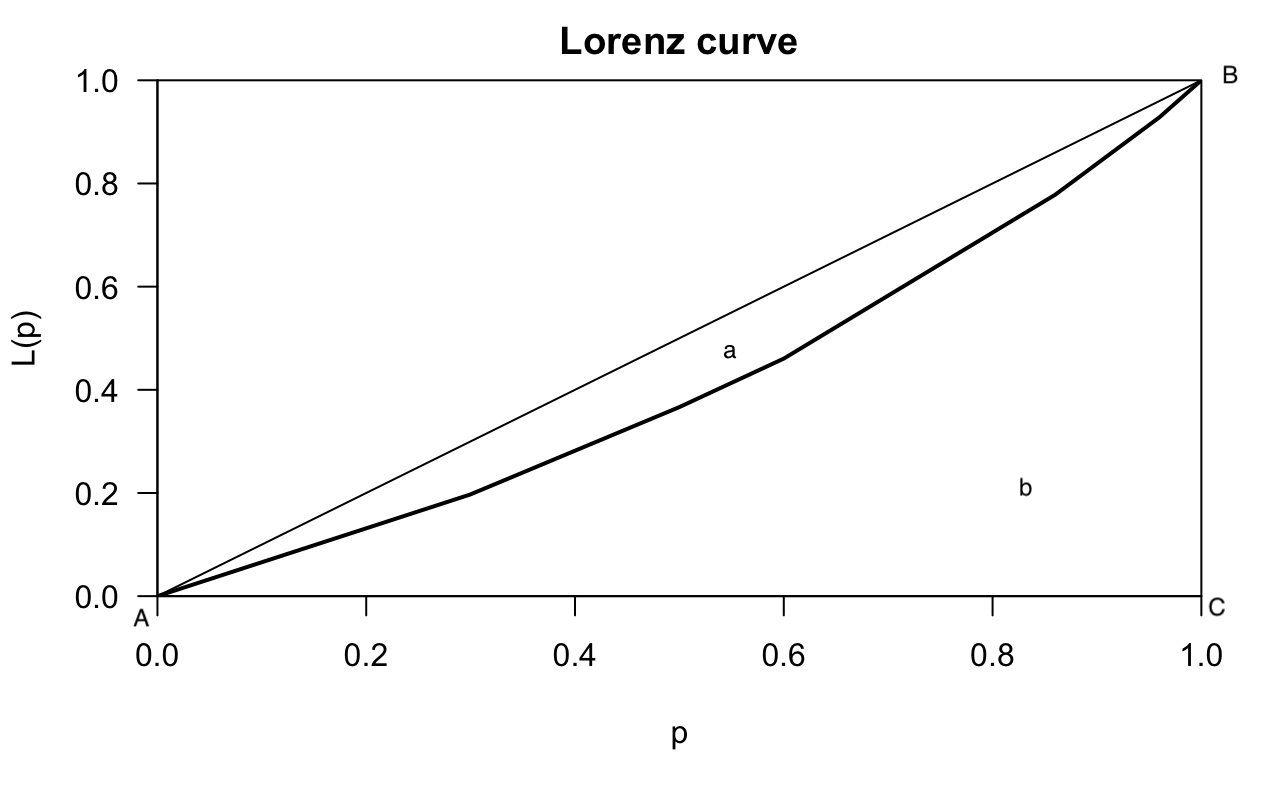
FIGURA 2.2: A curva de Lorenz com algumas indicações
A área que corresponde a letra \(a\) é denominada área de desigualdade. o seguimento de retas \(\overline{AB}\) é chamado de linha de perfeita igualdade onde \(p=\Phi\) e a área de de desigualdade é zero.
Analisando o casos de máxima desigualdade:
- excluindo-se o fato de renda negativa, considere que apenas um de \(n\) indíviduos receba toda a renda e os demais \(n-1\) indivíduos recebam zero de renda.
- Neste caso a pocentagem de renda é zero até o ponto \(\dfrac{n-1}{n}\) no eixo horizontal, tornando-se \(\Phi = 1\) ao se incluir o último indíviduo.
- Neste caso, a Curva de Lorenz é dada pela poligonal \(\widehat{ABC}\) e a área de desigualdade máxima é o triângulo \(ABC\).
2.4 Índice Gini
Considere os dados da tabela 2.1. Seja \(p\) o valor da proporção acumulada da população até certo estrato e seja \(\Phi\) o valor da correspondente proporção acumulada da renda. Os pares de valores \((p,\Phi)\), para os diversos estratos, definem pontos em um sistema de eixos cartesianos como aparece na figura 2.2. Estes pontos estão sobre a curva de Lonrez, que mostra como a porporção acumulada da renda \((\Phi)\) varia em função da proporção acumulada da população \((p)\), com as pessoas ordenadas de acordo com valores crescentes da renda. A área correspondente a \(a\) que está entre a reta AB e a curva de Lorenz na figura 2.2, é denominada área de desigualdade.
Para entender como ocorre a variação desta área de desigualdade, a área \(a\), primeiro considere uma situação de distribuição de renda com perfeita igualdade, ou seja, uma população em que todos recebem a mesma renda.Nesta situação, a uma população \(p\) da população corresponde uma igual proporção \(\Phi\) da renda total, ou seja, \(\Phi = p\). Portanto, a curva de Lorenz dessa distribuição coincide com a reta AB da figura 2.2, denominado, por isso, de linha de perfeita igualdade. Neste caso a área de desigualdade é igual a zero.
Considere agora uma outra situação, uma distribuição de renda com o máximo de desigualdade. Considerando que não existe a possibilidade de renda negativa, esse seria o caso de uma população com \(n\) pessoas, em que uma delas recebe toda a renda e as \(n-1\) restante receba zero de renda. Nesta situação, a proporção acumulada da renda é igual a zero até o ponto do eixo horizontal (abcissa) \(\frac{(n-1)}{n}\), tornando-se \(\Phi = 1\) quando se se inclui a pessoa que recebe toda a renda. Neste caso, a curva de Lorenz passa a ser a poligonal ABC da figura 2.2. Que é numericamente igual a 0,5 (Por quê?).
Por definição, o índice de Gini (G) é uma relação entre a área de desigualdade, indicada por \(a\) que passar a ser denominada de \(\alpha\), e a área do triângulo ABC que é numericamente igual a 0,5, ou seja,
\[ G = \dfrac{\alpha}{0,5} = 2\alpha \tag{2.1} \]
A fórmula (2.1) é uma das fórmulas de Gini que tem utilidade do ponto de vista teórico.Uma vez que
\[ 0 \leq \alpha \leq 0,5 \]
tem se que
\[ 0 \leq G \leq 1 \]
Ou seja de que o índice de Gini varia entre entre zero, ausência de desigualdade, e um, máxima desigualdade.Adicionalmente, o índice de Gini é um número adimensional.
Uma fórmula alternativa e mais prática do ponto de vista do cálculo do índice de Gini pode ser obitda considerando-se uma distribuição discreta.
Seja uma variável aleatória discreta \(X_i\) para \(i=1,\ldots,n\), cujos valores estão em ordem crescente
\[ X_1\leq X_2 \leq \ldots \leq X_{n-1} \leq X_n \] admitindo-se que os n valores são igualmente prováveis.
a proporção acumulada do número de elementos,m até o i-ésimo elemento, é
\[ p_i = \dfrac{i}{n},~\text{para}~i =1,\ldots, n \tag{2.2} \]
A correspondente proporção acumulada de \(X\), até o i-ésimo elemento é
\[ \Phi_i = \dfrac{\sum_{j=1}^{i}X_j}{\sum_{j=1}^{n}X_j} = \dfrac{1}{n\mu}\sum_{j=1}^{i}X_j \tag{2.3} \] onde \[ \mu = \dfrac{1}{n}\sum_{j=1}^{n}X_j \] Se \(X\) representa a renda individual e se \(X_j < X_{j+1}\), \(\Phi_i\) representa a fração da renda total apropriada pelas pessoas com renda inferior ou igual a \(X_i\). As expressões (2.2) e (2.3) definem as coordenadas \((p_i,\Phi_i)\) com \(i=1,\ldots, n\) de \(n\) pontos da curva de Lorenz. A rigor não existe, nesse caso, uma curva, mas uma poligonal cujos vértices são a origemdos exios e os pontos de coordenadas \((p_i,\Phi_i)\).
Na sequência é apresentada de forma resumida como se calcula o índice de Gini a partir dos valores de \(X_i\) para \(i = 1,\ldots ,n\) da variável. Na figura 2.2 a soma das áreas \(a\) e \(b\) totaliza a área do polígono ABC que numericamente é igual a 0,5. Portanto, \(a = 0,5 - b\). Ou seja, colocando na notação mais elegante,
\[ \alpha = 0,5 - \beta. \tag{2.4} \] Substituindo (2.4) em (2.1) obtém-se
\[ G = \dfrac{0,5 - \beta}{0,5} = 1 - 2\beta. \tag{2.5} \] Note que a área abaixo da “curva” de Lorenz pode ser representada, de forma aproximada, como a soma das áreas de \(n\) trapézios um do lado do outro. Desta forma, a área \(b\) da figura 2.2, compreendida entre a poligonal de Lorenz e o eixo das abscissas, é obtida somando-se a área dos \(n\) trapézios. Ou seja, a área do i-ésimo trapézio é \[ S_i = \dfrac{\Phi_{i-1} + \Phi_i}{2}\times \dfrac{1}{n} \tag{2.6} \] onde \(\Phi_{i-1}\) é a base menor do i-ésimo trapézio; \(\Phi_i\) é a base maior do i-ésimo trapézio e; \(1/n\) é a altura do trapézio que corresponde a pessoa da população composta por n pessoas.
Note que o valor de \(\Phi_0 = 0\), ou seja, o valor de \(\Phi_{i-1}\) para \(i=1\). Com base na fórmula (2.6) é possível obter a área corresponde a \(b\) na figura 2.2 ou \(\beta\) nas notações matemáticas no texto
\[ \beta = \sum_{i=1}^{n}S_i = \dfrac{1}{2n}\sum_{i=1}^{n}(\Phi_{i-1} + \Phi_i) \tag{2.7} \] Substituindo (2.7) em (2.5), obtém-se
\[ G = 1 - \dfrac{1}{n}\sum_{i=1}^{n}(\Phi_{i-1} + \Phi_i) \tag{2.8} \] Considerando a fórmula (2.3) e que \(\Phi_0 = 0\), se obtém o índice de Gini em termos da variável \(X_i\). Ou seja,
\[ G = 1 - \dfrac{1}{n^2\mu}[(2n-1)X_1 + (2n-3)X_2 + \dots + 3X_{n-1} + 1X_n] \tag{2.9} \]
Na parte sobre Estatística Descritiva foi apresentada a medida de dispersão chamada Diferença Absoluta Média que é dada por
\[ \Delta = \dfrac{1}{n^2}\sum_{i=1}^{n}\sum_{j=1}^{n}|X_i - X_j| \tag{2.10} \]
Trabalhando algebricamente a fórmula (2.10)
\[ \Delta = 2\mu - \dfrac{2}{n^2}[(2n-1)X_1 + (2n-3)X_2 + \dots + 3X_{n-1} + 1X_n] \tag{2.11} \]
Se dividir (2.11) por \(2\mu\) obtém a fórmula do índice de Gini em termos da medida de dispersão Diferença Absoluta Média
\[ G = \dfrac{\Delta}{2\mu} \tag{2.12} \]
Tratando-se da distribuição da renda em uma população, a relação (2.12) mostra que o índice de Gini, como medida de do grau de desigualdade, apresenta a vantagem de medir diretamente as diferenças de rendal, levando em consideração diferenças entre as rendas de todos os pares de pessoas.
Como \(\Delta\) é uma medida de dispersão da distribuição, a relação (2.12) mostra que o índice de Gini é uma medida de dispersão relativa. Assim, o conceito de desigualdade de uma distribuição se confunde com o conceito de dispersão relativa.
Com um desenvolvimento algébrico de \(\Delta\) é possível transformar a fórmula (2.12) em
\[ G = \dfrac{2}{n^2\mu}\sum_{i=1}^{n} iX_i - \dfrac{1}{n} - 1 \tag{2.13} \] A relação (2.13) mostra que, no cálculo do índice de Gini, cada valor de \(X_i\) da variável aparece poderado por \(i\). Ou seja, \(X_i\) aparece poderada pelo respectivo número de ordem na sequência dos valores ordenados.
Exemplo numérico
Para aplicar a fórmula do índice de Gini, utiliza-se os dados apresentados na tabela abaixo, obtidos de Hoffmann (2006).
| \(i\) | \(p_i\) | \(X_i\) | \(\sum_{j=1}^{n}X_j\) | \(\Phi_i\) | \(\Phi_{i-1} + \Phi_i\) |
|---|---|---|---|---|---|
| 1 | 0,125 | 1 | 1 | 0,02 | 0,02 |
| 2 | 0,250 | 1 | 2 | 0,04 | 0,06 |
| 3 | 0,375 | 1 | 3 | 0,06 | 0,10 |
| 4 | 0,500 | 2 | 5 | 0,10 | 0,16 |
| 5 | 0,625 | 4 | 9 | 0,18 | 0,28 |
| 6 | 0,750 | 8 | 17 | 0,34 | 0,52 |
| 7 | 0,875 | 13 | 30 | 0,60 | 0,94 |
| 8 | 1,000 | 20 | 50 | 1,00 | 1,60 |
Com essas informações é possível calcular o índice de Gini, através de (2.8)
\[ G = 1 - \dfrac{1}{n}\sum_{i=1}^{n}(\Phi_{i-1} + \Phi_i); \]
através de (2.12)
\[ G = \dfrac{\Delta}{2\mu}, \] onde \[ \Delta = \dfrac{1}{n^2}\sum_{i=1}^{n}\sum_{j=1}^{n}|X_i - X_j| \] e \[ \mu = \sum_{i=1}^{n}X_i; \] e através de (2.13)
\[ G = \dfrac{2}{n^2\mu}\sum_{i=1}^{n} iX_i - \dfrac{1}{n} - 1 \] Usando (2.8), é necessário totalizar a coluna \(\Phi_{i-1} + \Phi_i\) na tabela 2.2. Ou seja,
options(OutDec = ",")
somaphis <- c(0.02, 0.06, 0.1, 0.16, 0.28, 0.52, 0.94,
1.6)
somasomaphis <- sum(somaphis)
somasomaphis## [1] 3,68\[ \sum_{i+1}^{8} (\Phi_{i-1} + \Phi_i) = 3,68 \]
Portanto
giniphis <- 1 - 1/length(somaphis) * somasomaphis
giniphis## [1] 0,54\[ G = 1 - \dfrac{1}{8}\times 3,68 = 0,54 \]
Para aplicar a fórmula (2.12) que é a fórmula do índice de Gini em termos de diferença absoluta média, \(\Delta\), é necessário calcular a diferença absoluta média com base nos dados de \(X_i\) da tabela 2.2.
xi <- c(1, 1, 1, 2, 4, 8, 13, 20)
XC <- matrix(xi, nrow = length(xi), ncol = length(xi),
byrow = FALSE)
XC## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 1 1 1 1 1 1 1 1
## [2,] 1 1 1 1 1 1 1 1
## [3,] 1 1 1 1 1 1 1 1
## [4,] 2 2 2 2 2 2 2 2
## [5,] 4 4 4 4 4 4 4 4
## [6,] 8 8 8 8 8 8 8 8
## [7,] 13 13 13 13 13 13 13 13
## [8,] 20 20 20 20 20 20 20 20XL <- matrix(xi, nrow = length(xi), ncol = length(xi),
byrow = TRUE)
XL## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 1 1 1 2 4 8 13 20
## [2,] 1 1 1 2 4 8 13 20
## [3,] 1 1 1 2 4 8 13 20
## [4,] 1 1 1 2 4 8 13 20
## [5,] 1 1 1 2 4 8 13 20
## [6,] 1 1 1 2 4 8 13 20
## [7,] 1 1 1 2 4 8 13 20
## [8,] 1 1 1 2 4 8 13 20DIFX <- XC - XL
DIFX## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 0 0 0 -1 -3 -7 -12 -19
## [2,] 0 0 0 -1 -3 -7 -12 -19
## [3,] 0 0 0 -1 -3 -7 -12 -19
## [4,] 1 1 1 0 -2 -6 -11 -18
## [5,] 3 3 3 2 0 -4 -9 -16
## [6,] 7 7 7 6 4 0 -5 -12
## [7,] 12 12 12 11 9 5 0 -7
## [8,] 19 19 19 18 16 12 7 0ABSDIFX <- abs(DIFX)
ABSDIFX## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 0 0 0 1 3 7 12 19
## [2,] 0 0 0 1 3 7 12 19
## [3,] 0 0 0 1 3 7 12 19
## [4,] 1 1 1 0 2 6 11 18
## [5,] 3 3 3 2 0 4 9 16
## [6,] 7 7 7 6 4 0 5 12
## [7,] 12 12 12 11 9 5 0 7
## [8,] 19 19 19 18 16 12 7 0iota <- matrix(1, nrow = length(xi), ncol = 1, byrow = TRUE)
iota## [,1]
## [1,] 1
## [2,] 1
## [3,] 1
## [4,] 1
## [5,] 1
## [6,] 1
## [7,] 1
## [8,] 1somacolunaABSDIFX <- t(iota) %*% ABSDIFX
somacolunaABSDIFX## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 42 42 42 40 40 48 68 110somalinhasomacolunaABSDIFX <- somacolunaABSDIFX %*%
iota
somalinhasomacolunaABSDIFX## [,1]
## [1,] 432obs <- length(xi)
delta <- obs^(-2) * somalinhasomacolunaABSDIFX
delta## [,1]
## [1,] 6,75Ou seja,
\[ \Delta = \dfrac{1}{n^2}\sum_{i=1}^{n}\sum_{j=1}^{n}|X_i - X_j| = \dfrac{1}{(8)^2} \times 432 = 6,75 \]
Com a diferença absoluta média de \(X_i\) devidamente calculada, aplica-se a fórmula (2.12)
ximedio <- sum(xi)/length(xi)
ximedio## [1] 6,25ginidelta <- delta/(2 * ximedio)
ginidelta## [,1]
## [1,] 0,54\[ G = \dfrac{\Delta}{2\mu} = \dfrac{6,75}{2 \times 6,25} = 0,54 \]
Para aplicar a fórmula (2.13) na obtenção do índice de Gini é necessário ponderar cada valor de \(X_i\) pela sua respectiva ordem \(i\) e soma todos os respectivos produtos
\[ \sum_{i=1}^{n}iX_i. \]
usando os dados da tabela 2.2
is <- matrix(1:length(xi), nrow = length(xi), ncol = 1,
byrow = TRUE)
is## [,1]
## [1,] 1
## [2,] 2
## [3,] 3
## [4,] 4
## [5,] 5
## [6,] 6
## [7,] 7
## [8,] 8ixi <- t(is) * xi
ixi## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 1 2 3 8 20 48 91 160somaixi <- sum(ixi)
somaixi## [1] 333ginifinal <- 2/(obs^2 * ximedio) * somaixi - obs^(-1) -
1
ginifinal## [1] 0,54obtém
\[ G = \dfrac{2}{n^2\mu}\sum_{i=1}^{n} iX_i - \dfrac{1}{n} - 1 = \dfrac{2}{8^2 \times 6,25}\times 333 - \dfrac{1}{8} - 1 = 0,54 \]
2.5 Discrepância Máxima
Discrepância Máxima é a maior distância entre entre a linha AB e a curva de Lorenz da figura 2.2. Portanto, a discrepância máxima é a diferença máxima entre a relação da porcentagem acumulada da população e a sua respectiva porcentagem acumulada da renda numa situação de exata igualdade dada pela reta AB e a relação da porcentagem acumulada da população e a sua respectiva porcentagem acumulada da renda numa situação de desigualdade entre as pessoas dessa população que na figura corresponde a poligonal da curva de Lorenz. De acordo com Hoffmann (2006)
\[ D = p_h - \Phi_h \tag{2.14} \]
Portanto, o cálculo de \(D\) através de (2.14) depende de \(h\), um número inteiro positivo. Encontrando-se \(i=h\) encontra-se a discrepância máxima \(D\).
Seja uma sequência de valores ordenados em ordem crescente de uma variável discreta \(X_i\)
\[ X_1 \leq X_2 \leq \ldots \leq X_n \]
sendo válida pelos menos uma desigualdade.
Para o cálculo da discrepância máxima, é importante entender que a mesma ocorre quando a inclinação do segmento da poligonal da curva de Lorenz passa de uma valor menor que um para um valor maior que um. De acordo com Hoffmann (2006), a inclinação do segmento da poligonal é dada por
\[ d_i = \dfrac{X_i}{\mu} \]
Essa mudança é identificada quando o valor de \(X_i\) ordenada em ordem crescente passa de uma valor menor que a média \(\mu\) para um valor maior que a média \(\mu\), ou seja,
\[ X_i < \mu~~para~1 \leq i \leq h \] e \[ X_i \geq \mu~~para~h < i \leq n \]
Nesaas condições percorre-se a sequência de valores em ordem crescente, o valor de \(p_i - \Phi_i\) aumenta até a inclusão do h-ésimo elemento.que corresponde a (2.14).
Considerando (2.14), (2.2) e (2.3) chaga-se em
\[ D = \dfrac{h}{n} - \dfrac{1}{n\mu}\sum_{i=1}^{h}X_i \] que depois de algumas manobras algébricas torna-se
\[ D = \dfrac{1}{n\mu}\sum_{i=1}^{h}(\mu - X_i) \tag{2.15} \] Na parte de estatística descritiva foi apresentado a medida de dispersão desvio absoluto médio
\[ \delta = \dfrac{1}{n}\sum_{i=1}^{n}|X_i - \mu| \] e considerando que \[ \delta = \dfrac{1}{n}\left[ -\sum_{i=1}^{h}\left(X_i - \mu\right) + \sum_{i=h+1}^{n}\left(X_i - \mu\right)\right] \] e que \[ \sum_{i=h+1}^{n}\left(X_i - \mu\right) = -\sum_{i=1}^{h}\left(X_i - \mu\right). \] Portanto \[ \delta = \dfrac{2}{n}\sum_{i=h+1}^{n}\left(X_i - \mu\right) = \dfrac{2}{n}\sum_{i=1}^{h}\left(\mu - X_i \right). \tag{2.16} \] Comparando (2.16) e (2.15) obtém-se
\[ D = \dfrac{\delta}{2\mu}. \tag{2.17} \] Se o Desvio Absoluto Médio, \(\delta\), é uma medida de dispersão da distribuição, a fórmula (2.17) mostra que discrepância máxima, da mesma forma que o índice de Gini, é uma medida de dispersão relativa. Retomando o exemplo numérico da tabela 2.2, é possível obter o valor da sua discrepância máxima através de (2.14).
\[ D = p_h - \Phi_h = 0,625 - 0,180 = 0,445. \] O mesmo resultado poderia ser obtido através da fórmula (2.17). Para isso é necessário calcular o desvio absoluto médio, \(\delta\), para os valores de \(X_i\) do exemplo numérico. Ou seja,
somadesvioabsolutomedioxi <- sum(abs(xi - ximedio))
somadesvioabsolutomedioxi## [1] 44,5desvioabsolutomedioxi <- (length(xi))^(-1) * sum(abs(xi -
ximedio))
desvioabsolutomedioxi## [1] 5,5625\[ \delta = \dfrac{1}{n}\sum_{i=1}^{n}|X_i - \mu| = \dfrac{1}{8}\times 44,5 = 5,5625. \] Portanto,
discrepanciamaximaxi <- desvioabsolutomedioxi/(2 *
ximedio)
discrepanciamaximaxi## [1] 0,445\[ D = \dfrac{\delta}{2\mu} = \dfrac{5,5625}{2 \times 6,25} = 0,445. \]
2.6 Redundância e Índice de Theil
2.6.1 Teoria da Informação
Para entender melhor as medidas de desigualdades de Theil, é necessário introduzir alguns conceitos da teoria da informação.
Seja \(x\), a probabilidadde de ocorrer o evento \(E\).
Para \(x=1\), a mensagem evento \(E\) ocorreu não tem nenhum conteúdo informativo.
Para \(x \rightarrow 0\), ou seja, para valores muito pequenos de \(x\), a mensagem evento \(E\) ocorreu tem alto valor informativo.
A segunda situação seria, por exemplo, o caso de uma notícia que nos causas surpresa ou de um furo de imprensa. Quando \(x\) tende a zero, o conteúdo informativo da mensagem evento \(E\) ocorreu tende a infinito.
Matematicamente, o conteúdo informativo da mensagem que afirma que determinado evento ocorreu é dado por
\[ h(x) = \log \dfrac{1}{x} = \log x^{-1} = - \log x \tag{2.18} \]
De acordo com Hoffmann (2006), a escolha da função logarítmica é devido a propriedade de atividade do conteúdo informativo no caso de eventos independentes. Portanto, se \(E_1\) e \(E_2\) são dois eventos independentes com probabilidades \(x_1\) e \(x_2\), respectivamente, a probabilidade de que ambos ocorram é \(x_1x_2\). O conteúdo informativo da mensagem de que ambos os eventos ocorreram é
\[ h(x_1x_2) = \log \dfrac{1}{x_1x_2} = \log\dfrac{1}{x_1} + \log \dfrac{1}{x_2} = h(x_1) + h(x_2) \] Em teoria da informação, normalmente se utiliza logarítmos na base 2 ou logarítmos naturais. Desta forma:
Logaritmos na base 2: o conteúdo informativo é medido em bits.
Logaritmos naturais: o conteúdo informativo é medido em nits.
1 bit = 0,693 nit.
1 nit = 1,443 bit.
Generalizando o conceito de informação, é apresentando, na sequência, como se mede o conteúdo informativo de uma mensagem sujeita a erro, ou mensagem incerta.
Para isso, admita-se que a a probabilidade de chover em um determinado dia, em certo local, estabelecida com base em séries históricas, seja \(x_1 = 0,5\). Nesse caso o conteúdo da informação chove é de
\[ h(x_1) = \log\dfrac{1}{0,5} =\log 2^1 = 1~\text{bit} \] Suponha agora que uma previsão de tempo estabeleceu que iria chover. Suponha, também, que, com base nos resultados anteriores de tais previsões, probabilidade de que realmente shova passa a ser \(y_1 = 0,68\). De acordo com as novas suposições, o conteúdo da informação chove é
\[ h(y_1) = \log\dfrac{1}{o,68} + 0,5564~\text{bit} \]
O conteúdo informativo da previsão é
\[ h(x_1) - h(y_1) = \log\dfrac{1}{x_1} - \log\dfrac{1}{y_1} = 1 - 0,5564 = 0,4436~\text{bit} \] ou \[ h(x_1) - h(y_1) = \log\dfrac{1}{x_1} - \log\dfrac{1}{y_1} = \log\dfrac{1}{x_1} + \log \left(\dfrac{1}{y_1}\right)^{-1} = \log\dfrac{y_1}{x_1} = \log\left(\dfrac{0,50}{0,68}\right) = 0,4436~\text{bit}. \] Ou seja, o conteúdo informativo chove, com base na probabilidade \(x_i\) nos dados históricos e na probabilidade \(y_i\) do histórico de previsões, é de 0,4436 bit.
Generalizando, o coanteúdo informativo de uma mensagem sujeita a erro ou mensagem incerta, como é o caso da previsão, é dado por
\[ \log \dfrac{y}{x} \tag{2.19} \] onde
\(x\) é a probabilidade ex-ante ou a probabilidade de que o evento ocorra antes de recebida a mensagem;
\(y\) é a probabilidade ex-post ou a probabilidade de que oevento ocorra uma vez recebida a mensagem.
Na sequência é apreseantado o conceito de entropia.
Entropia de uma distribuição \(H(x)\)
Seja o universo de \(n\) possíveis eventos \(E_i\), para \(i=1,\ldots ,n\), mutuamente exclusivos aos quais associa-se as probabilidades \(x_i\). Sabe-se que
\[ \sum_{i}^{n} x_i = 1. \]
A informação esperada de uma mensagem certa, ou seja, a esperança matemática do conteúdo informativo da mensagem ocorreu \(E_i\), também denominada entropia da distribuição, é
\[ H(x) = E[h(x_i)] = \sum_{i=1}^{n} x_i h(x_i) = \sum_{i=1}^{n}x_i \log\dfrac{1}{x_i} = - \sum_{i=1}^{n}x_i \log x_i \tag{2.20} \]
Para o caso particular de \(x_i= 0\), adota-se a definição \[ x\log x = 0,~~\text{se}~x = 0 \tag{2.21} \] uma vez que \[ \lim_{x\rightarrow 0}(x\log x) = 0 \] Para \(0 < x_i \leq 1\) se tem
\[ \dfrac{1}{x_i}\geq 1 \]
e
\[ \log \dfrac{1}{x_i} \geq 0. \] Conclui-se que \[ H(x) = \sum_{i=1}^{n} x_i \log \dfrac{1}{x_i} = - \sum_{i=1}^{n} x_i \log x_i \geq 0 \]
Valor mínimo de \(H(x)\)
O valor mínimo de \(H(x)\) ocorre quando uma das probabilidades é 1 e as demais, consequentemente, são nulas. Nesse caso \(H(x) = 0\). Ou seja, na somatória há um único \(x_i=1\) e o restante \(x_i = 0\). Portanto,
quando \(x=0\) \[ x \log x = 0 \] de acordo com (2.21);
quando \(x=1\) se tem \(\log 1 = 0\) e também \[ x \log x = 0. \]
Assim o valor mínimo do valor esperado do conteúdo informativo \(H(x)\) é
\[ H(x) = - \sum_{i=1}^{n}x_i \log x_i = 0 \]
Valor Máximo de \(H(x)\)
Para encontrar o valor máximo de \(H(x)\) sujeito a condição de que \(\sum x_i = 1\), utiliza-se o método do multiplicador de Lagrange, escrevendo a seguinte função
\[ \max H(x) = -\sum_{i=1}^{n}x_i \log x_i \] sujeito a \[ \sum_{i=1}^{n} x_i = 1 \] então \[ \mathcal{L} = -\sum_{i=1}^{n}x_i \log x_i - \lambda\left( \sum_{i=1}^{n} x_i - 1 \right) \tag{2.22} \] Igualando a zero as derivadas parciais de (2.22) em relação a \(x_i\) e admitindo-se que se usa os logaritmos naturais, se tem:
\[ \log x_i = -(1 + \lambda),~~para~i=1,\ldots ,n \] sendo que \[ x_i = e^{-(1+\lambda)} = \dfrac{1}{e^{(1+\lambda)}}. \]
Note que \(\lambda\) é constante neste caso.
O valor máximo de \(H(x)\) acontece quando todos os valores de \(x_i\), ou seja, todos as probabilidades são iguais entre si e, portanto, igual a \(\dfrac{1}{n}\). Nesse caso,
\[ H(x) = \sum_{i=1}^{n} x_i \log \dfrac{1}{x_i} = \sum_{i=1}^{n} \dfrac{1}{n} \log n = n \dfrac{1}{n}\log n = \log n \]
Resumindo, o valor esperado da informação ou a entropia da distribuição \(H(x)\) varia entre 0 e \(\log n\). Ou seja,
\[ 0\leq H(x) \leq \log n. \tag{2.23} \]
A entropia da distribuíção é máxima, ou seja, há um máximo de incerteza a respeito do que pode ocorrer, quando todos os possíveis eventos são igualmente prováveis, ou seja, quando há um máximo de desordem no sistema.
Informação de uma mensagem incerta
Finalmente é apresentado o conceito de informação de uma mensagem incerta. Dado o universo de \(n\) possíveis eventos \(E_i\), mutuamente exclusivos, com probabilidades \(x_i\), para \(i=1, \ldots, n\), considera-se uma mensagem incerta que poderia ser uma previsão ou uma mensagem duvidosa, que transforma as probabilidades a priori \(x_i\) em probabilidade a posteori \(y_i\), onde \(y_i\) é a probabilidade de ocorrência do evento \(E_i\) depois de recebido a mensagem. Lembrando (2.19), verifica-se que a esperança matemática do conteúdo informativo da mensagem é
\[ I(y:x) = \sum_{i=1}^{n} y_i \log\dfrac{y_i}{x_i} \tag{2.24} \]
A definição (2.18), do conteúdo informativo de uma mensagem certa, é somente um caso especial de (2.24), eem que uma probabilidade a posteriori é igual a um e todas as outras são iguais a zero, ou seja, \(y_j = 1\) e \(y_i = 0\) para todo \(i\neq j\).
2.6.2 Índice T de Theil
Seja uma população com \(n\) pessoas em que cada uma recxebe uma fração não negativa da renda total,
\[ y_i \geq 0,~~com~i=1,\ldots ,n. \] Se a renda média é \(\mu\) e \(X_i\) é a renda i-ésima pessoa, \[ y_i = \dfrac{X_i}{n\mu}. \] Obviamente, \[ \sum_{i=1}^{n} y_i = 1. \] Os valores de \(y_i\) tem as mesmas propriedades que as probabilidades \(x_i\) associadas a um universo de eventos \(E_i\) da teoria da informação. Assim sendo, pdoe-se, com base em (2.20), definir a entropia da distribuição de renda considerada como sendo \[ H(y) = \sum_{i=1}^{n} y_i \log \dfrac{1}{y_i}. \] De acordo com (2.23), se tem
\[ 0\leq H(y) \leq \log n. \] Assim é possível definir as duas situações extremas:
o caso de perfeita igualdade na distribuição da renda, \[ y_i = \dfrac{1}{n}~~para~i=1, \ldots, n, \] se tem \(H(y) = \log n\);
o caso de perfeita desigualdade na distribuição de renda, \[ y_i = 1,~~para~i=1, \ldots, n, \] se tem \(H(y) = 0\).
A entropia é, portanto, uma medida do grau de igualdade da distribuição. Mas como o objeto de análise é desigualdade, é ,muito mais interessante uma medida de desigualdade. Para isto basta subtrair a entropia do seu valor próprio máximo, \(\log n\). Essa medida, denominada Índice T de Theil da distribuição é dada por
\[ T = \log n - H(y) = \sum_{i=1}^{n}y_i \log n y_i \tag{2.25} \] Para o cálculo do índice T de Theil, pode-se usar os logarítmos naturais ou os logarítmos na base 2, obtendo-se o valor de T en nits ou bits, respectivamente. Na prática, utiliza-se mais o logarítmo natural.
Note que
\[ 0 \leq T \leq \log n \tag{2.26} \] sendo que:
\(T = 0\) corresponde ao caso de uma distribuição da renda com perfeita igualdade e;
\(T = \log n\) corresponde ao caso de uma distribuição da renda com perfeita desigualdade.
De (2.25) se tem
\[ T = \sum_{i=1}^{n}y_i \log \dfrac{y_i}{\dfrac{1}{n}}. \]
Comparando essa equação com (2.24), verifica-se que o índice T de Theil corresponde à esperança do valor informativo de uma mensagem incerta, em que as probabilidades a posteriori são as frações da renda total \(y_i\) apropriadas pelas pessoas, e as probabilidades a priori são iguais a \(1/n\), ou seja, iguais à fração da população correspondente a cada pessoa.
2.6.3 Índice de L de Theil
A outra medida de desigualdade proposta por Theil, o índice L de Theil, corresponde à esperança do valor informativo de uma mensagem incerta, em que as probabilidades 8a posteriori* são as frações da população \(1/n\) e as probabilidades a priori são as frações da renda \(y_i\). Ou seja,
\[ L = \sum_{i=1}^{n}\dfrac{1}{n} \log \dfrac{\dfrac{1}{n}}{y_i} = \dfrac{1}{n}\sum_{i=1}^{n} \log \dfrac{1}{ny_i}. \tag{2.27} \] Verifica-se que o índice L de Theil é igual a zero no caso de pefeita igualdade \[ y_i = \dfrac{1}{n} \] para todo \(i\).
Basta uma das renda aproximar-se de zero para que o valor de \(L\) tenda a infinito, fazendo que o índice \(L\) seja inútil quando se trata de comparar distribuições de renda que incluem valores nulos.
Uma vantagem importante das medidas de desigualdades de Theil na análise da distribuição de renda ou da riqueza é que, quando os dados podem ser agrupados com base em um critério qualquer, por exemplo regiões, os valores de \(T\) e \(L\) podem ser decompostos em uma medida de desigualdade entre grupos, por exemplo inter-regional, e uma média poderada das medidas de desigualdades dentro de grupos, por exemplo dentro das regiões.
2.7 Variância dos Logaritmos
A variância dos logaritmos das rendas é frequentemente utilizada como medida da desigualdade da distribuição da renda em uma população. Para uma população com \(n\) pessoas, em que a renda da \(i\)-ésima pessoas aé indicada por \(X_i\) para \(i=1, \ldots, n\), a variância dos logaritmos das rendas é dada por
\[ V(Z) = \dfrac{1}{n} \sum_{i=1}^{n} \left( Z_i - \overline{Z} \right)^2 \tag{2.28} \] onde \[ Z_i = \log X_i \] e \[ \overline{Z} = \dfrac{1}{n}\sum_{i=1}^{n} Z_i. \] Nota-se que \(V(Z)\) só e definida para \(X_i \geq 0\) para \(i=1, \ldots, n\).
Indicando-se por \(X^*\) a média geométrica dos \(X_i\) , se tem
\[ V(Z) = \dfrac{1}{n} \sum_{i=1}^{n} \left( \log \dfrac{X_i}{X^*} \right)^2 \tag{2.29} \]
A variância dos logaritmos, da mesmaforma que as medias \(T\) e \(L\) de Theill, é uma medida de desigualdade que, quando os dados podem ser agrupados segundo um critério qualquer, pode ser decomposta em um componente que corresponde à desigualdade entre os grupos e uma média podenrada das variâncias dos logarítmos dentro dos grupos.